Handreiking voor gedegen reken-wiskundeonderwijs!
Doen in de les (handelend rekenen)
Gecijferdheid als doel
De nieuwe rekeneisen MBO (2022) gaan uit van functionele en realistische situaties. Dat zijn situaties die herkenbaar zijn in het dagelijks leven van de student of voor het beroep waarvoor hij/zij wordt opgeleid. De eisen zijn zo opgesteld dat ze gedrag beschrijven: “de eisen kennen de vorm van descriptoren. Daarbij gaat het om denkactiviteiten en handelingen van studenten op het gebied van rekenen in de breedste zin van het woord. Dat gaat minder om technisch rekenen (‘kale sommen’) en veel meer om bijvoorbeeld het interpreteren van informatie of het opstellen en uitvoeren van een plan van aanpak om een probleem op te lossen” (ECBO).
De nieuwe kerndoelen rekenen-wiskunde (PO/VO) hebben expliciet aandacht voor wiskunde en de wereld. Direct in de inleiding wordt gecijferdheid als doel van reken-wiskundeonderwijs benoemd. Daarvoor is het oefenen van sommen een middel, en geen doel op zich.
“Gebruiken en begrijpen van wiskunde, waaronder rekenen, is belangrijk voor het functioneren in de samenleving, bij het uitoefenen van een beroep en voor het maken van keuzes in het persoonlijke leven. Om kansengelijkheid te bevorderen moeten alle leerlingen hiervoor een goede basis meekrijgen. Alle leerlingen moeten vlot en wendbaar leren rekenen en zich ontwikkelen tot gecijferde burgers. Gecijferdheid, oftewel wiskundige geletterdheid, stelt mensen in staat om de werkelijkheid te begrijpen en informatie op waarde te schatten. In het funderend onderwijs leren leerlingen met wiskunde informatie en verschijnselen in de wereld om hen heen op eigen niveau te doorgronden. Het herkennen en gebruiken van wiskunde in bekende en nieuwe situaties draagt bij aan hun verdere wiskundige ontwikkeling” (SLO, 2023).
Dit betekent dat je in een ISK ook het rekenen kan inbedden in functionele situaties die leerlingen kunnen tegenkomen in het dagelijks leven. Hierbij sluit je aan bij de belevingswereld van de leerlingen en dus ook bij de doelen binnen het vervolgonderwijs.
Je kunt hiermee ook een link leggen naar lessen Burgerschap, LOB en andere vakken. Zie ook handreiking Burgerschap.
- Soms hebben MBO’s nog eigen rekeneisen bij instroom. Goed om daar kennis van te hebben (en rekening mee te houden of het gesprek over aan te gaan).
- Naarmate het uitstroomniveau hoger is, ligt het accent meer op wiskunde dan op rekenen. Maar het handelend rekenen mag niet vergeten worden als middel voor differentiatie.
Differentiatie
Door de grote onderlinge verschillen tussen leerlingen binnen de ISK-klassen is differentiëren noodzakelijk. Omdat de leerdoelen in moeilijkheidsgraad oplopen kun je in een les op verschillende niveaus aan hetzelfde doel werken. Denk aan optellen tot 10, tot 100 en met grote getallen.
- Start de les samen, met een gemeenschappelijk onderwerp/domein/doel.
- Voor tips zie artikel Differentiëren in rekenonderwijs.
- Verwerking daarna op eigen niveau:
- Lesdoelen binnen het rekenen bouwen zich op binnen een domein. Eerst leer je optellen tot tien, dan over het tiental, dan tot honderd, waarbij tientaloverschrijding lastiger blijft dan sommen die binnen een tiental blijven. Als je werkt aan optellen kun je leerlingen daardoor na de instructie op eigen niveau laten verwerken door sommige leerlingen optelsommen tot 1000 te geven en anderen sommen tot 100 zonder tientaloverschrijding. Je kunt de focus dan bijvoorbeeld wel behouden op het kiezen van een strategie.
- Door opgaven meer open te stellen, vragen te stellen waarop meer antwoorden mogelijk zijn, kunnen leerlingen op hun eigen niveau antwoorden. “Schrijf een som op waarvan het antwoord 96 is”. Teken een figuur waarvan de oppervlakte 24 is”.
- In het filmpje “low floor high ceiling” legt Jo Boaler uit waarom dit soort opgaven een mooie manier zijn om leerlingen rekenconcepten beter te leren en ook te differentiëren in de les. Het filmpje gaat over het verschil tussen antwoordgerichte vragen en procesgerichte vragen die meer ruimte geven om te leren en denken over reken-wiskundeconcepten. De opgaven bieden veel ruimte om op eigen niveau te antwoorden, en het bespreken van de antwoorden biedt meteen veel ruimte voor het versterken van de rekentaal.
- Kies bij de verwerking na de instructie wat passender is, werken op papier of met de computer. Beide vormen hebben hun eigen voor- en nadelen.
- Gezamenlijke evaluatie: volgen van het proces, wat heeft de leerling geleerd?
- Differentieer van concreet naar abstract, zie handelingsmodel.
- 2- Sporenbeleid:
- Route 1 en 2 blijft meer concreet.
- Route 3 sneller meer abstract (formeel rekenen).
- Afwisseling in werkvormen:
- Instructie en verwerking.
- Binnen/in de les en buiten/vakintegratie en gecijferdheid.
- Denk aan spelletjes.
- Zelf vragen maken bij een doel (‘productief oefenen’).
- Op papier of op de computer.
- Links naar methodes:
- Openbaar toegankelijke materialen:
- Poster met ‘10 tips voor een meertalige aanpak in jouw (reken)les’ van het Alfa-college.

Doen in de school
Naast de reken-wiskundelessen, is het advies om ook in andere lessen aandacht te besteden aan praktische opdrachten die de gecijferdheid bevorderen (2de spoor). Het is belangrijk dit in alle routes te doceren. Routeafhankelijk kan ‘eenzelfde’ praktische opdracht makkelijker of moeilijker gemaakt worden.
- Maak gebruik van verschillende werkvormen tijdens je lessen. Activeer leerlingen.
- Start bijvoorbeeld met meten, omdat je hier goede materialen handelend bij kan inzetten. Zo kan je gemakkelijker taal koppelen aan visuele ondersteuning en relevante begrippen aanleren.
- Een aanzet met voorbeelden die binnen de school uitvoerbaar zijn:
- Neem folders mee uit je brievenbus, laat leerlingen een collage maken:
- Wat zijn procenten?
- Voorbeelden uit het dagelijks leven.
- Huiswerkopdracht: maak foto’s van concrete situaties waarin je het rekenprobleem dat behandeld wordt tegenkomt in de wereld om je heen:
- Waar zie je procenten?
- Zorg voor meet- en weegattributen:
- Behandel lengte en oppervlakte door bijvoorbeeld het meten van je eigen lijf, de klas en de school.
- Maak met plakband een vierkante meter in het lokaal.
- Hoever is het lopen naar de supermarkt?
- Hoever is de afstand naar het land van herkomst?
- Bereid een kookles voor (bijvoorbeeld wafels of pepernoten bakken).
- Gewicht en inhoud.
- Zet spelletjes in. Er zijn veel gezelschapsspellen waar rekenvaardigheid voor nodig is. Bekijk ook eens Spel in de rekenles of Rondje rekenspel.
- Maak gebruik van de praatplaten (en andere ideeën en expertise) van Gecijferdheid telt mee.
- Houd een rekendialoog.
- Benut de rekenthema’s op bladzijde 68-74 van de rekeneisen MBO.
- Neem folders mee uit je brievenbus, laat leerlingen een collage maken:
Voorbeelden uit het dagelijks leven
Naar de supermarkt
Je gaat naar de supermarkt:
- Hoeveel kg aardappels kun je kopen met 5 euro?
- Je hebt 4 euro en koopt 1 kg paprika. Hoeveel geld heb je nog over?
- Hoeveel kost het om vier courgetten te kopen?
- Welke producten kun je kopen met 10 euro? (Meerdere antwoorden mogelijk)
Wanneer een leerling moeite heeft met kale sommen, is het een optie om de leerling een rekenmachine te geven. Zelfs met een rekenmachine, is het belangrijk om te weten wat de stappen zijn om een sommetje op te lossen. Dus, kan een leerling een rekenmachine benuttigen wanneer optrekken, aftrekken, etc. zelf doen, te moeilijk is.

Dialoog: reizen
- Hoi, weet jij toevallig hoeveel het kost om met de NS van Maastricht naar Amsterdam te gaan?
- Oh… dat weet ik niet uit mijn hoofd. Ik zal even op de NS app kijken. Ik zie dat het in totaal 29,40 euro kost.
- Dat is best duur! Ik heb alleen 20 euro meegenomen. Is er een andere mogelijkheid?
- Ja, je bent jonger dan achttien jaar, dus kun je een dag ticket kopen voor 7,90 euro.
- Geweldig! Dan houd ik ook nog 12,10 euro over (20,00 – 7,90 = 12,10).
- Tot ziens!

Dialoog: kopen
- Hallo, zou u mij kunnen helpen?
- Natuurlijk! Wat is uw vraag?
- Ik heb een bed nodig, maar ik weet niet welke ik moet kopen.
- Hmm… wat is de lengte en breedte van uw kamer?
- De lengte van mijn kamer is 3 meter en de breedte van mijn kamer is 2 meter.
- Oke. Dit bed is geschikt voor uw kamer. Hij is 90 cm breed en is 200 cm lang.
- Prima! Ik zal het kopen.

Dialoog: pizza bestellen
(Telefoongesprek)
- Hallo! Ik zou een pizza willen bestellen. Hoeveel kost een pizza?
- Hallo, een pizza kost tien euro. Vandaag is er een korting van 50% op elke 2de pizza, wanneer het bezorgd wordt.
- Oke. Zou ik dan twee pizza’s kunnen bestellen?
- Ja, natuurlijk. Dan moet u 15 euro betalen.
- Prima. Bedankt!

Doen buiten de school
Rekenen en wiskunde stopt niet buiten het klaslokaal. Je kunt in de les gebruik maken van situaties in het echte leven maar bedenk ook dat je in het echte leven gebruik moet maken van je reken-wiskundekennis uit de klas.
- Ga naar buiten, sluit aan bij de echte wereld, voorbeelden die uitvoerbaar zijn:
- Ga boodschappen doen, maak een lijstje, bedenk hoeveel geld je nodig hebt en neem geld mee om echt te betalen.
- Ga naar de dichtstbijzijnde bushalte en kijk hoe laat de bus vertrekt en waar die heen gaat.
- Zoek op internet uit wat de beste route is naar … met het OV en waarom.
- Loop 1 kilometer. Hoe lang doe je daar over? Is het ver?
- Benut de rekenthema’s op bladzijde 68-74 van de rekeneisen MBO.

Kies je doelen zorgvuldig
Op de ISK is maar beperkte tijd om alle reken-wiskundevaardigheden aan te leren. Bedenk vooraf welke onderdelen weggelaten zouden kunnen worden. Doe eens iets NIET. Durf onderwerpen over te slaan. Denk aan de volgende overwegingen:
- Moeten leerlingen de tafels uit hun hoofd kennen?
- Neem het dagelijks leven als uitgangspunt, wat heb je nodig om je te redden in de samenleving?
- Verbied de rekenmachine NIET; maak er gebruik van:
- Bij vrijwel al het rekenen en in de wiskunde in het VO, MBO 1 en MBO 2 is een rekenmachine toegestaan.
- In het dagelijks leven heeft iedereen de hele dag zijn telefoon bij de hand, niemand vraagt je op straat hoeveel 7 x 5 is.
- Verbied niet het denken in en gebruiken van de eigen taal:
- Natuurlijk is Nederlands leren een belangrijk doel in de ISK.
- Tijdens de reken-wiskundeles is naast het rekenen-wiskunde ook de taal een doel, zowel in het Nederlands als in de thuistaal:
- Het kan helpen de eigen taal als denktaal te gebruiken. (Presentatie Thuistalen in de rekenles)
- Belangrijk is om daar ook het Nederlands aan toe te voegen. Zie ook Taal in rekenen en zie Kerndoel 23 (PO) en Kerndoel 19 (VO): de leerlingen leren passende wiskundetaal gebruiken.
- Redeneren en formuleren bij wiskunde vakken slo
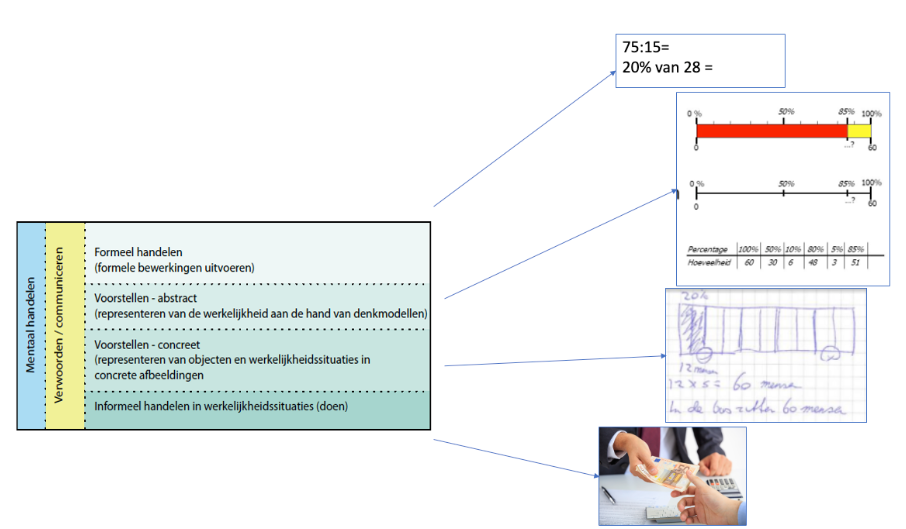
Van concreet naar abstract (en terug)
Benut het handelingsmodel rekenen. De handelingsniveaus lopen van concreet naar abstract. Door te handelen in de werkelijkheid met concrete materialen binnen een context, kun je veel taal toevoegen aan een situatie en ook met gebaar en materiaal goed duidelijk maken wat er gebeurt.
Hiermee kan vrijwel iedereen de situatie en de rekenhandeling volgen en begrijpen. Denk aan het betalen met geld en het teruggeven van wisselgeld, of het tellen van tafelgroepjes in de klas. Je kunt ook denken aan het echt meten van afstanden of werken met stapels en rijen verpakkingen uit de supermarkt.
Het wordt abstracter door afbeeldingen van contexten te gebruiken, hierdoor is de handeling nog wel voorstelbaar maar niet concreet te zien. Je bouwt de mate van abstractie verder op door minder materialen en modellen in te zetten of tekeningen te gebruiken waardoor je niet meer in het echt kunt tellen. Het meest abstract is de ‘kale som’.
Hierdoor moet het rekenwerk in ieders hoofd gebeuren en is minder steun van materiaal of model. Door steeds de (kale) som in verband te brengen met de concrete situatie en/of de weergave met materiaal neem je leerlingen mee in de overeenkomst en oplossing van de opgave. Zo koppel je de som aan de echte situatie: Hoe schrijven we dit in rekentaal?
Andersom kun je leerlingen ook echte situaties laten bedenken bij een ‘kale som’. Waar zou deze som over kunnen gaan? 5 x 3 kan dan gaan over blikken tennisballen, maar ook over hoeveel bootjes er nodig zijn bij het schoolreisje of het aantal maaltijden in een werkweek. Laat de leerlingen zelf eens op zoek gaan naar rekenen-wiskunde in hun omgeving. Misschien kunnen ze foto’s maken van situaties waar ze sommen in herkennen. Zo laat je de breedte (en realiteit) van wiskunde zien en koppel je de ‘kale sommen’ uit de klas aan het echte leven.
Meer informatie over het handelingsmodel vind je in het protocol ERWD www.erwd.nl en op www.elbd.sites.uu.nl.
Veel voorbeelden van lessen waarin dit idee wordt uitgewerkt zijn te vinden op de LOWAN website primair onderwijs, op basis van de rekenkisten die door het ABC zijn samengesteld.